(Extraído de: [1] "Statistical Analysis of Network Data with R")
4.1 Introducción
En el estudio de un sistema complejo determinado, pueden surgir preguntas de interés sobre aspectos de la estructura o características del grafo correspondiente. Tradicionalmente, el análisis estructural de un grafo se ha tratado como una tarea descriptiva, en lugar de una tarea inferencial, y las herramientas comúnmente utilizadas para tales propósitos derivan en gran parte de áreas que están fuera de la estadística "convencional". Por ejemplo, una proporción abrumadora de estas herramientas provienen principalmente del campo de la teoría de grafos y por lo tanto tienen sus orígenes en la matemática e informática. En este capítulo se presenta una breve descripción general de algunas de las muchas herramientas disponibles, comenzando con un resumen de las características de los vértices y aristas, en la sección 4.2, continuando con las medidas de cohesión de una red, en la sección 4.3, y con métodos para la partición de grafos, en la sección 4.4, y terminando con los temas de assortividad y mezcla, en la sección 4.5.
4.2 Características de los vértices y aristas
4.2.1 Grado de un vértice
El grado $d_v$ de un vértice $v$, en un grafo $G = (V, E)$, cuenta el número de aristas en $E$ que inciden
sobre $v$. Dado un grafo $G$, se define $f_d$ como la fracción de vértices $v \in V$ con grado $d_v = d$. La
colección $\lbrace f_d \rbrace$ con $d \geq 0$ se llama distribución de grados de $G$, y es simplemente un cambio de
escala del conjunto de frecuencias de grados, formado a partir de la secuencia de grados
original. La distribución de grados para el grafo del club de karate (Figura 4.1.2) se muestra a
continuación usando un histograma.
1 > library(igraph)
2 > library(sand)
3 > data(karate)
4 > hist(degree(karate), col="lightblue", xlim=c(0, 50),
5 + xlab="Grado del vértice", ylab="Frecuencia", main="")
Figura 4.1.1
Donde el grafo cuenta con la siguiente estructura:6 > plot(karate)
Figura 4.1.2
Podemos ver que los dos vértices más conectados corresponden a los actores 1 y 34 del grafo,
representando al instructor y administrador. Donde los grados de los vértices son:
> degree(karate)
Mr Hi Actor 2 Actor 3 Actor 4 Actor 5 Actor 6 Actor 7 Actor 8 Actor 9
16 9 10 6 3 4 4 4 5
Actor 10 Actor 11 Actor 12 Actor 13 Actor 14 Actor 15 Actor 16 Actor 17 Actor 18
2 3 1 2 5 2 2 2 2
Actor 19 Actor 20 Actor 21 Actor 22 Actor 23 Actor 24 Actor 25 Actor 26 Actor 27
2 3 2 2 2 5 3 3 2
Actor 28 Actor 29 Actor 30 Actor 31 Actor 32 Actor 33 John A
4 3 4 4 6 12 17
Para grafos ponderados, una generalización útil de grado es la noción de fuerza del vértice,
que se obtiene simplemente sumando los pesos de las aristas incidentes a un vértice dado. La
distribución de la fuerza a veces denominada distribución de grados ponderados, es definida en
analogía con la distribución de grados ordinaria. A continuación, con el siguiente histograma
podemos ilustrar, la fuerza del vértice para el grafo del club de karate.
1 > hist(graph.strength(karate), col="pink",
2 + xlab="Fuerza del vértice", ylab="Frecuencia", main="")
Figura 4.1.3
Para este grafo, el rango de la fuerza del vértice se extiende mucho más allá del grado del
vértice, y se pierde la distinción observada anteriormente entre los tres grupos de vértices
(Figura 4.1.1). Sin embargo, se podría decir que ambos histogramas comunican información
importante sobre el grafo. Nota: Entre las métricas aplicables a grafos ponderados tenemos como medida la ya
mencionada fuerza del vértice.
Las distribuciones de grados pueden exhibir una variedad de formas. Para una red de
interacciones entre pares de proteínas en levadura, por ejemplo:
1 > library(igraphdata)
2 > data(yeast)
4 > d.yeast <- degree(yeast)
5 > hist(d.yeast,col="blue",
6 + xlab="Grado", ylab="Frecuencia",
7 + main="Distribución de grados")
Figura 4.1.4
En particular, si bien hay una fracción sustancial de vértices de grado bastante bajo, de un orden
de magnitud similar a los del grafo del club de karate, también hay un número no trivial de
vértices con grados en órdenes de magnitud sucesivamente superiores.
Además del histograma presentado(Figura 4.1.4), una escala logarítmica es efectiva al resumir
la información, donde obtenemos:
Más allá de la distribución de grados en sí, puede ser interesante comprender como se enlazan
vértices de diferentes grados entre sí. Esta característica es la noción de grado medio de los vecinos de un vértice dado. Por ejemplo, una gráfica del grado de vecinos promedio versus
grado del vértice en los datos de levadura, como se muestra a continuación, sugiere que, si bien
existe una tendencia a vértices de grados más altos para enlazar con vértices similares, los
vértices de grado más bajo tienden a enlazarse con vértices de grados inferiores y superiores.
1 > a.nn.deg.yeast <- graph.knn(yeast,V(yeast))$knn
2 > plot(d.yeast, a.nn.deg.yeast, log="xy",
3 + col="goldenrod", xlab=c("Grado del vértice(escala logarítmica)"),
4 + ylab=c("Grado de vecino promedio(escala logarítmica)"))
4.2.2 Centralidad de un vértice
La centralidad es una medida de la importancia relativa de un vértice dentro del grafo. Esta importancia no es una propiedad intrínseca del vértice, si no que viene determinada por la posición de éste en el grafo.Existen múltiples métricas que permiten determinar la centralidad de un vértice. Estas métricas se clasifican en dos grupos: métricas radiales y mediales. En las métricas radiales el vértice en cuestión es origen o destino de caminos generados con un cierto criterio, y la métrica de centralidad determina la cantidad de caminos existentes (métrica de volumen) o la longitud de estos (métrica de longitud). Sin embargo, en las métricas mediales se emplea para determinar la centralidad de los vértices y la cantidad de caminos que atraviesan dicho vértice.[2] Algunas de las métricas de centralidad más importantes son la centralidad de grado, de cercanía, de proximidad y de vector propio.
- Centralidad de grado
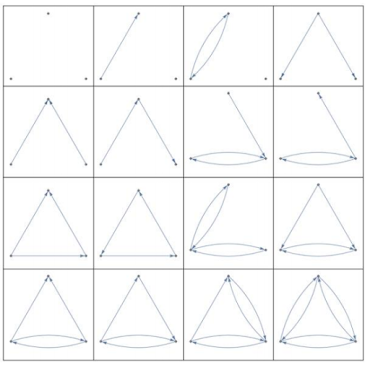
La centralidad de grado es una medida radial de volumen que se calcula como el número de aristas incidentes en el vértice. Esta medida da una idea de la conectividad de un vértice. La siguiente figura muestra la escala de centralidad de grado de los vértices de un grafo, en una escala en la que mayor oscuridad significa mayor centralidad. [2]
Figura 4.1.7, [2]. Aplicación de teoría de grafos a redes con elementos
autónomos.
- Centralidad de cercanía
La centralidad de cercanía es una métrica radial de longitud calculada como la inversa del
valor medio de las distancias mínimas desde ese vértice al resto de vértices del grafo. Por tanto,
cuanto mayor sea la distancia media menor será la centralidad del vértice y viceversa [2]. Las medidas de centralidad de cercanía intentan capturar la noción de que un vértice es
central 'si está cerca' de muchos otros vértices.
El enfoque estándar, introducido por Sabidussi , es dejar que la centralidad varíe inversamente
con una medida del total de la distancia de un vértice a todos los demás,
$$C_{Cl}(V)= \frac{1}{\sum_{u\in V} dist(v,u)},$$
Donde $dist (v,u)$ es la distancia geodésica (camino más corto) entre los vértices ${u,v\in V}$. Esta media esta entre el intervalo $[0,1]$, mediante la multiplicación por un factor $N_{v-1}$.
- Centralidad de intermediación
La centralidad de intermediación es una medida de centralidad medial que viene dada por la
fracción de caminos más cortos entre vértices del grafo que atraviesan el vértice en cuestión [2]. En otras palabras, las medidas de centralidad de intermediación tienen como
objetivo resumir hasta qué punto un vértice se encuentra "entre" otros pares de vértices. Estas
centralidades se basan en la perspectiva de que la 'importancia' se relaciona con la ubicación de
un vértice con respecto a las rutas en el grafo, puesto que es probable que haya rutas más críticas
para el proceso de comunicación.
$$C_{B}(V)= \sum_{s\neq t\neq v \in V}\frac{\sigma (s,t\mid v)}{\sigma (s,t)},$$
Donde $\sigma (s,t\mid v)$ es el número total de caminos más cortos entre $s$ y $t$ que pasan a través de $v$ , y $\sigma (s,t)$ es el número total de caminos más cortos entre $s$ y $t$ (independiente de si pasan o no por $v$). En el caso de que los caminos más cortos sean únicos, $C_{B}(V)$ solo cuenta el número de caminos más cortos que pasan por $v$ . Esta medida de centralidad puede estar restringida al intervalo unitario mediante la división por un factor de $( N_{v - 1}) ( N_{v - 2}) / 2$.
Finalmente, otras medidas de centralidad se basan en nociones de "estatus" o "prestigio" o "rango". Es decir, buscan capturar la idea de que cuanto más centrales son los vecinos de un vértice, más central es ese vértice en sí. Estas medidas están implícitas de forma inherente en su definición y, por lo general, pueden expresarse en términos de soluciones de vectores propios de sistemas lineales de ecuaciones adecuadamente definidos.
- Centralidad de vector propio
Hay muchas medidas de centralidad del vector propio . Por ejemplo, Bonacich , siguiendo el trabajo de Katz y otros, definieron una medida de centralidad de la forma:
$$C_{Ei}(v)= \alpha \sum_{ \lbrace u,v \rbrace\in E } {C_{Ei}(u)}.$$
El vector $C_{Ei}={(C_{Ei}(1), . . . ,C_{Ei}(N_v))}^T$ es la solución del problema de valor propio $A_{C_{Ei}}={\alpha}^{-1}$, donde $A$ es la matriz de adyacencia para el grafo $G$, Bonacich argumenta que una elección óptima de ${\alpha}^{-1}$ es el valor propio más grande de $A$ , y por tanto $C_{Ei}$es el vector propio correspondiente.
Cuando $G$ no es dirigido y conexo, el valor propio más grande de $A$ será simple (multiplicidad algebraica 1) y el vector propio correspondiente tendrá todas sus entradas distintas de cero y compartiendo el mismo signo. Las entradas automáticamente estarán entre 0 y 1 por la ortonormalidad (conjunto ortogonal y la norma de cada uno de sus vectores es igual a 1) de vectores propios.
Una forma intuitivamente atractiva de mostrar centralidades de vértices (para grafos de tamaño pequeño a moderado) es utilizar un diseño radial, con más vértices centrales ubicados más cerca del centro. La función gplot.target , en el paquete sna , se puede utilizar para este propósito. Por ejemplo,
2 > library(network)
3 > g <- network::as.network.matrix(A)
4 > library(sna)
5 > sna::gplot.target(g, degree(g), main="Degree",
6 + circ.lab = FALSE, circ.col="skyblue",
7 + usearrows = FALSE,
8 + vertex.col=c("blue", rep("red", 32), "yellow"),
9 + edge.col="darkgray")
produce una visualización de la centralidad de grado para el grafo del club de karate, como se muestra en la Figura 4.1.8
Figura 4.1.8
La aplicación de estas medidas a una red de blogs sobre el SIDA indica, que solo 6 de los 146 blogs de esta red desempeñan el papel de hub, mientras que la vasta mayoría de los vértices (incluidos algunos de los hubs) desempeñan el papel de una autoridad.
4.2.3 Caracterización de aristas
Si nos preguntamos por qué los lazos en una red social son los más importantes para la difusión
de, digamos, información o rumores. Podemos comprender que el concepto de centralidad de
arista se relaciona con la centralidad del vértice, por ejemplo, la centralidad de intermediación de aristas, se extiende sobre la centralidad de intermediación de vértices de una manera sencilla, asignando a cada arista un
valor que refleja el número de caminos más cortos que atraviesan dicha arista.
4.3 Caracterización de la cohesión en una red
Hay muchas formas en que podemos definir la cohesión de una red, dependiendo del contexto de la pregunta que se hace. Las definiciones difieren, por ejemplo, en escala, de rango local (por ejemplo, tríadas) a global (por ejemplo, componentes gigantes), y también en la medida en que se especifican explícitamente (p. ej., cliques (camarillas)) versus implícitamente (p. ej., 'grupos' o 'comunidades'). En esta sección discutimos una serie de formas comunes de definir y resumir la "cohesión" en una red.
4.3.1 Subgrafos y censos
Un enfoque para definir la cohesión de una red es mediante la especificación de un cierto subgrafo de interés. El ejemplo canónico de tal subgrafo es el de una camarilla. Recuerde que las camarillas son subgrafos completos y, por tanto, son subconjuntos de vértices que son totalmente cohesivo, en el sentido de que todos los vértices dentro del subconjunto están conectados por aristas. Un censo de camarillas nos permite tener una idea de cómo está estructurado el grafo como en este caso el grafo del club de karate:
2
3 1 2 3 4 5
4 34 78 45 11 2
Para el grafo del club de karate, un censo de este tipo refleja que hay 34 nodos (camarillas de tamaño uno) y 78 aristas (camarillas de tamaño dos), seguidos de 45 triángulos (camarillas de tamaño tres), etc. Pero hay cierta redundancia en este análisis, ya que las camarillas de más tamaño incluyen necesariamente camarillas de tamaños más pequeños. Una camarilla máxima es una camarilla que no es un subconjunto de una camarilla más grande. Por ejemplo, en el grafo del club de karate hay dos camarillas máximas.
2
3 2 3 4 5
4 11 21 2 2
En la práctica las camarillas máximas son relativamente raras. Para conocer el tamaño de la camarilla máxima (formalmente llamada, numero de camarilla), usamos la siguiente instrucción:
1 > clique.number(karate)2 [1] 5
Además, es popular para la visualización, usar la noción de núcleos, ya que proporciona una forma de descomponer una red en capas (como una cebolla), esto se pueden combinar de una manera particularmente efectiva con un diseño radial, por ejemplo, en el caso del grafo del club de karate:
1 > cores <- graph.coreness(karate)2 > sna::gplot.target(g, cores, circ.lab = FALSE,
3 + circ.col="skyblue", usearrows = FALSE,
4 + vertex.col=cores, edge.col="darkgray")
5 > detach("package:network")
6 > detach("package:sna")
Figura 4.2.2, Representación visual de la descomposición de k-core del grafo del club de karate, los vértices del núcleo uno están representados en color negro, dos (rojo),tres (verde) y cuatro (azul), se muestran distancias sucesivamente más pequeñas desde el centro, con las mismas distancias para los vértices dentro de cada núcleo.
Más allá de las camarillas y sus variantes, existen otras clases de subgrafos de interés general
en definir la cohesión de una red. Dos cantidades fundamentales (análisis de redes sociales), que
son las díadas y tríadas.
Las diadas son pares de vértices que, en grafos dirigidos, puede tomar tres estados posibles:
nulo (sin aristas dirigidas), asimétrico (una arista dirigida) o mutuo (dos aristas dirigidas).
En cambio, las tríadas pueden tomar 16 estados posibles, como lo podemos observar en el
siguiente gráfico:
Figura 4.2.3
Un censo de los posibles estados de estas dos clases de subgrafos, es decir, contando cuántas veces se observa cada estado en un grafo $G$ , puede dar una idea de la naturaleza de la conectividad en un grafo. Por ejemplo, en la red de blogs sobre el SIDA (Figura 4.1.9), vemos que la gran mayoría de diadas son nulas, mientras de las que no son nulas, casi todas son asimétricas, lo que indica la clara unilateralidad con la que los blogs en la red se hacen referencia entre sí.
1 > aidsblog <- simplify(aidsblog)2 > dyad.census(aidsblog)
3 mut
4 [1] 3
5
6 asym
7 [1] 177
8
9 null
10 [1] 10405
Como podemos observar este análisis es consistente con las observaciones del análisis anterior de hubs y autoridades en esta red.
Podemos efectuar un censo de cualquier subgrafo de internes. Los pequeños subgrafos de interés conexos se denominan comúnmente motivos, ejemplos de estos motivos, son subgrafos con una estructura en forma de abanico (varias aristas dirigidas que emanan de un solo vértice) y bucles de avance (es decir, tres aristas rectas, entre tres vértices, de la forma $\lbrace u, v \rbrace$, $\lbrace v, w \rbrace$ y $\lbrace u, w \rbrace$ ). En una red enumerar estas apariciones puede llevar bastante tiempo. Por lo que se utiliza métodos de muestreo, con recuentos de motivos estimados, usando la función graph.motifs.
4.3.2 Densidad y nociones relacionadas de frecuencia relativa
La densidad de un grafo es la relación entre el número de aristas del grafo y el número de
aristas máximo, el cual es el número de aristas de un grafo completo con el mismo número de
vértices. Por ejemplo, en un grafo $G$ (no dirigido) sin bucles automáticos y sin múltiples aristas,
la densidad de un subgrafo $H = ( V_H , V_H )$ es
$$den(H)= \frac{\vert E_H \vert}{\vert V_H \vert (\vert V_H \vert - 1)/2},$$
El valor de $den(H)$ estará entre cero y uno (la densidad máxima es 1 (para un grafo completo) y la densidad mínima es de 0 ), proporcionando una medida de que tan cerca está $H$ de ser una camarilla. En el caso de que $G$ sea un dígrafo, el denominador se sustituye por ${\vert V_H \vert (\vert V_H \vert - 1)}$.
El concepto posiblemente simple de densidad se vuelve interesante a través de la libertad que tenemos en la elección del subgrafo $H$. Por ejemplo, tomando $H = G$ se obtiene la densidad del grafo general G . Por el contrario, tomando $H = H_V$ como el conjunto de vecinos de un vértice $v \in V$ , y las aristas entre ellos, da una medida de densidad en la vecindad inmediata de $v$.
Aplicando estas ideas al grafo del club de Karate, por ejemplo, vemos que, en los subgrafos correspondientes a cada uno de los instructores y administradores, en unión con sus respectivos vecindarios inmediatos, es decir, las redes egocéntricas alrededor vértices 1 y 34: son notablemente más densos que la red general.
2 + neighborhood(karate, 1, 1)[[1]])
3 > ego.admin <- induced.subgraph(karate,
4 + neighborhood(karate, 1, 34)[[1]])
5 > graph.density(karate)
6 [1] 0.1390374
7 > graph.density(ego.instr)
8 [1] 0.25
9 > graph.density(ego.admin)
10 [1] 0.209150
Lo cual es consistente con el grafo:
Figura 4.2.4
La frecuencia relativa también se utiliza para definir las nociones de "agrupación" en un grafo.
Por ejemplo, el uso estándar del término coeficiente de agrupamiento típicamente se refiere a
la cantidad
$$cl_{T}(G)= \frac{3\tau_\bigtriangleup (G)}{\tau_3 (G)},$$
donde $\tau_\bigtriangleup(G)$ es el número de triángulos en el grafo $G$ , y $\tau_3(G)$, es el número de triples conectados (es decir, un subgrafo de tres vértices conectados por dos aristas, también a veces llamado 2-star). El valor $cl_T(G)$ es llamado transitividad del grafo, y es una cantidad estándar de interés en la literatura de redes sociales ,donde también se conoce como la "fracción de triples transitivos". Hay que tener en cuenta que $cl_T(G)$ es una medida de agrupamiento global, que resume la frecuencia relativa con la que los triples conectados se acercan para formar triángulos. Por ejemplo, en el grafo del club de karate vemos que sólo alrededor de una cuarta parte de los triples conectados se cierran de esta manera.
1 > transitivity(karate)
Nota: el efecto percolación se produce cuando se llega un punto en el que los diferentes
componentes aislados se unen.
Donde, la comunidad más grande es de 18
miembros y está centrada alrededor del
administrador (es decir, John A, ID de
vértice 34). La segunda comunidad más grande es de
11 miembros y se centra en el instructor
principal (es decir, el Sr.Hi, ID de
vértice 1).
La jerarquía resultante normalmente se representa en forma de un árbol, llamado dendrograma (organiza los datos en subcategorías que se van dividiendo en otros hasta llegar al nivel de detalle deseado asemejándose a las ramas de un árbol que se van dividiendo en otras sucesivamente). Este tipo de representación permite apreciar claramente las relaciones de agrupación entre los datos e incluso entre grupos de ellos, aunque no las relaciones de similitud o cercanía entre categorías. Observando las sucesivas subdivisiones podemos hacernos una idea sobre los criterios de agrupación de los mismos, la distancia entre los datos según las relaciones establecidas, etc. Como podemos ver a continuación:
Por ejemplo, las proteínas que se encuentran agrupadas en un grafo de proteínas entre las acciones a menudo participan en procesos biológicos similares; de manera similar, los actores agrupados en una red social pueden compartir ciertos intereses. La partición de grafos puede verse como una herramienta para descubrir dichos subconjuntos en la ausencia de conocimiento de estas características. Cuando tengamos conocimiento de alguna noción definida externamente de pertenencia a una clase, puede ser interesante comparar y contrastar las asignaciones resultantes con las que se derivan de la partición de grafos.
2 [1] 0.2556818
Respecto a los dígrafos, un concepto exclusivo es el de la reciprocidad, es decir, el grado de
reciprocidad entre lazos en una red dirigida, en otras palabras, la reciprocidad es una medida
de la probabilidad de que los vértices de una red dirigida se vinculen mutuamente entre sí .
Una forma tradicional de definir la reciprocidad $r$ es usando la proporción de número de enlaces
que apuntan en ambas direcciones ${L}^{<->}$ en el número total de enlaces L.[3]
$$r = \frac{L^{<->}}{L}$$
Con esta definición, $r = 1$ hace referencia a una red puramente bidireccional, mientras que $r = 0$ para una puramente unidireccional. En general las redes reales tienen un valor intermedio
entre 0 y 1.
Sin embargo, esta definición de reciprocidad tiene algunos defectos. No puede distinguir la
diferencia relativa de reciprocidad en comparación con una red puramente aleatoria con el
mismo número de vértices y aristas. La información útil de la reciprocidad no es el valor en sí
mismo, sino si los vínculos mutuos ocurren más o menos a menudo de lo que se espera por azar.
Además, en las redes que contienen auto-bucles (enlaces que empiezan y terminan en el mismo
vértice), estos deben excluirse al calcular L.
Hay dos principales enfoques, distinguidos por si la unidad de interés en el cálculo de
frecuencias relativas es el de díadas o aristas dirigidas. En el caso que las díadas se utilicen
como unidades, la reciprocidad se define como el número de díadas con aristas directas
recíprocas (es decir, mutuas) dividido por el número de díadas con una sola arista no
correspondida. Alternativamente, la reciprocidad se define como el número total de aristas
recíprocas dividido por el número total de aristas. En la red de blogs sobre el SIDA, la
reciprocidad es bastante baja, como se nota a continuación :
1 > reciprocity(aidsblog, mode="default")
2 [1] 0.03278689
3 > reciprocity(aidsblog, mode="ratio")
4 [1] 0.01666667
Recordando nuestro censo de díadas de la misma red, este resultado no es sorprendente, debido
a que teníamos 177 diadas asimétricas (unilaterales) y apenas 3 diadas mutuas.
1 > aidsblog <- simplify(aidsblog)
2 > dyad.census(aidsblog)
3 mut
4 [1] 3
5
6 asym
7 [1] 177
2 > dyad.census(aidsblog)
3 mut
4 [1] 3
5
6 asym
7 [1] 177
4.3.3 Conectividad, cortes y flujos
Se dice que un grafo $G$ es conexo si cada vértice es accesible entre sí, y que una componente
de un grafo es un subgrafo conectado al máximo, es decir que, el subgrafo en si es conexo, pero
no es conexo con otros subgrafos .
Nota: Un grafo no dirigido es conexo si existe un camino entre cada par de vértices y un grafo
dirigido se denomina fuertemente conexo si existe un camino desde cualquier vértice a cualquier otro vértice, además un grafo no conexo $G$ se puede partir de una sola forma en un
conjunto de subgrafos conexos y cada uno de ellos es una componente conexa de $G$.
A menudo en el caso de que una de las componentes conexas en un grafo $G$ domina a otras en
magnitud y contiene la gran mayoría de los vértices en $G$ . Tal se llama componente gigante,
es decir, un grupo de vértices enlazados entre sí, y que agrupan a la mayoría de los vértices de
la red.
Recordando, el ejemplo de la red de interacciones de proteínas en levadura, sabemos que la red
de 2617 vértices no es conexa.
1 > is.connected(yeast)
2 [1] FALSE
Sin embargo, un censo de todas las componentes conexas dentro del grafo muestra claramente
que existe una componente gigante
1 > comps <- decompose.graph(yeast)
2 > table(sapply(comps, vcount))
3
4 2 3 4 5 6 7 2375
5 63 13 5 6 1 3 1
Como apreciamos este componente tiene $2375/2617≈90\%$ de los vértices de la red. Por el
contrario, ninguno de los otros componentes por si solo tiene siquiera el $1\%$. En la práctica, a
menudo la atención se limitaría a este componente gigante para llevar a cabo más análisis de
modelado.
Por ejemplo, una característica célebre observada en el componente gigante de muchas redes
del mundo real es la llamada propiedad del mundo pequeño , que se refiere a la situación en la
que (a) la distancia de ruta más corta entre pares de vértices es generalmente bastante pequeña,
(b) la agrupación es relativamente alta. En nuestra red de interacciones proteicas en levadura,
vemos que la longitud media del camino en la componente gigante es apenas mayor de cinco.
1 > yeast.gc <- decompose.graph(yeast)[[1]]
2 > average.path.length(yeast.gc)
3 [1] 5.09597
Incluso el camino más largo no es muy extenso.
1 > diameter(yeast.gc)
2 [1] 15
Por lo tanto, la distancia de la ruta más corta en esta red se considera “Pequeña”, al mismo
tiempo, la agrupación en esta red es relativamente grande.
1 > transitivity(yeast.gc)
[1] 0.4686663
Lo que indica que cerca del $50\%$ de los triples conectados se cierran para formar triángulos.
Nota: La instrucción transitivity mide la probabilidad de que los vértices adyacentes de un
vértice estén conectados. A veces, esto también se denomina coeficiente de agrupamiento.
Una noción de conectividad algo más refinada que la de los componentes se deriva preguntando
si, un subconjunto arbitrario de k vértices (aristas) se elimina de un grafo, el subgrafo restante
está conectado. Los conceptos de conectividad de vértice, arista ,y los conceptos relacionados
de cortes de vértice y arista, ayudan a precisar tales nociones.
Un grafo $G$ se llama k-vértice-conectado si (i) el número de vértices $N_v>k$ , y (ii) la eliminación
de cualquier subconjunto de vértices $X ⊂ V$ de cardinalidad $\vert X \vert < k $ deja un subgrafo que está
conectado. De manera similar, $G$ se llama k-arista-conectada si (i) $N_v ≥ 2$, y (ii) la eliminación
de cualquier subconjunto de aristas $Y ⊆ E$ de cardinalidad $\vert Y \vert < k$ deja un subgrafo que está
conectado.
En el caso de la componente gigante de la red de proteínas en levadura, la conectividad respecto
al vértice y arista es igual a uno
1 > vertex.connectivity(yeast.gc)
2 [1] 1
3 > edge.connectivity(yeast.gc)
4 [1] 1
Por lo tanto, se requiere la eliminación de un solo vértice o arista bien elegida para dividir este
subgrafo en componentes adicionales . Si la eliminación de un conjunto particular de vértices o arista en un grafo desconecta el grafo,
ese conjunto se denomina corte de vértice . Un solo vértice que se desconecta se llama vértice
de corte o, a veces, punto de articulación. La identificación de tales vértices puede proporcionar
una idea de dónde una red es vulnerable (por ejemplo, en el sentido de un ataque, donde
desconectarse produce consecuencias no deseadas, como un corte de energía en una red de
energía eléctrica).
En la componente gigante de la red proteínas en levadura, casi el $15\%$ de los vértices son
vértices de corte.
1 > yeast.cut.vertices <- articulation.points(yeast.gc)
2 > length(yeast.cut.vertices)
3 [1] 350
Un resultado fundamental en la teoría de grafos, conocido como teorema de Menger,
esencialmente nos dice, sean $u,v \in V_G$ (con $V_G$ conjunto de vértices de un grafo), la cantidad de
vértices en $uv$ - corte mínimo es igual a la máxima cantidad de $uv$ – caminos
internamente ajenos.
Nota: Para profundizar en el enunciado y demostración del teorema de Menger así como en los conceptos de corte mínimo y caminos internamente ajenos visite el siguiente enlace: https://www.youtube.com/watch?v=39R7nDI9KcU&t=292s
Por lo tanto, el teorema de Menger relaciona la robustez de un grafo ante la eliminación de sus
vértices (aristas) con la máxima cantidad de distintos caminos que lo recorren. Por lo tanto, un
grafo con conectividad de vértices (aristas) puede tener rutas y, en consecuencia, contener
información fluyendo sobre esos caminos, lo cual puede ser interrumpido por la eliminación
apropiada de un pequeño número de vértices (aristas). Funciones como shortest.paths,
graph.maxflow, y graph.mincut se pueden usar en igraph para calcular cantidades relevantes
para esta conexión entre cortes y flujos.
4.4 Particionamiento de grafos
La partición, en términos generales, se refiere a la segmentación de un conjunto de elementos en
subconjuntos 'naturales'. Más formalmente, una partición $\mathscr{C} = \lbrace C_1,...,C_k \rbrace$ de un conjunto finito $S$ es
una descomposición de $S$ en $K$ subconjuntos no vacíos, disjuntos $C_k$ tal que $U_{k=1}^{K} C_k=S.$
La partición es una herramienta útil para encontrar, subconjuntos de vértices que demuestran una
'cohesión' con respeto a los patrones relacionales subyacentes.
Un subconjunto 'cohesivo' de vértices generalmente se toma para referirse a un subconjunto de vértices
que (i) están bien conectados entre sí, y al mismo tiempo (ii) están relativamente bien separado de los
vértices restantes.
Es decir, el objetivo del particionamiento de grafos es que, dado un grafo de $v$ vértices completamente
conexos y sus aristas con un peso determinado. El objetivo es dividir un grafo en $K$ subgrafos. Todos
estos subgrafos deben tener incorporados a lo menos 2 vértices y a lo más el doble de los vértices que
habría de existir en cada subgrafo si se divide el grafo total en $K$ subgrafos de igual cantidad de vértices.
La principal idea y final es que estos subgrafos al quedar conectados entre sí por aristas tengan el menor
grado de cohesión posible, es decir, que las aristas que unen los subgrafos pesen lo menos posible y de
esa manera poder evitar una cierta “dependencia trascendental” entre ellos.
4.4.1 Agrupación jerárquica
Una gran cantidad de métodos para la partición de grafos son esencialmente variaciones de
los conceptos más generales de agrupamiento jerárquico utilizado en el análisis de datos.
Hay numerosas técnicas que se han propuesto para el problema general de agrupamiento,
centrándose principalmente en (i) cómo evalúan la calidad de las agrupaciones propuestas y(ii)
los algoritmos mediante los cuales buscan optimizar esa calidad.
Podemos observar dos tipos de técnicas de agrupamiento jerárquico:
- Técnicas aglomerativas: comenzar con cada caso como un cluster individual. En cada paso, combinar el par de clusters más cercano hasta que sólo quede uno o k. [4]
- Técnicas divisivas: comenzar con un único cluster que englobe todos los casos de nuestro conjunto de datos. En cada paso, partir un cluster hasta que cada cluster contenga un único caso (o queden k clusters). [4]
En cada etapa, la partición candidata se modifica de una manera que minimiza una medida
especificada de costo. En los métodos aglomerativos, la combinación menos costosa de dos
elementos de partición previamente existentes se ejecuta, mientras que, en los métodos
divisivos, se ejecuta la división menos costosa de un solo elemento de partición existente en dos. La medida de costo incorporada en un método de agrupamiento jerárquico utilizado
en la partición de grafos debe reflejar nuestro sentido de lo que define un subconjunto 'cohesivo'
de vértices. Se han propuesto muchas medidas de costos. Una popular medida es la de
modularidad.
La modularidad es una medida de la estructura de las redes o grafos. Fue diseñado para medir
la fuerza de la división de una red en módulos (también llamados grupos, agrupamientos o
comunidades). Las redes con alta modularidad tienen conexiones sólidas entre los vértices
dentro de los módulos, pero escasas conexiones entre vértices en diferentes módulos. La
modularidad se utiliza a menudo en los métodos de optimización para la detección de la
estructura comunitaria de las redes. Sin embargo, se ha demostrado que la modularidad sufre
un límite de resolución y, por lo tanto, no es capaz de detectar pequeñas comunidades. Las redes
biológicas, incluidos los cerebros animales, presentan un alto grado de modularidad.
Un enfoque rápido y ávido de optimización en forma de un algoritmo de agrupamiento
jerárquico aglomerativo, es implementado en igraph como fastgreedy.community.
Aplicando este método al grafo del club de karate:
1 > kc <- fastgreedy.community(karate)
Observamos que tenemos 3 comunidades
1 > length(kc)
2 [1] 3
Y sus tamaños respectivos
3 > sizes(kc)
4 Community sizes
5 1 2 3
6 18 11 5
Basado en lo que sabemos de esta red y examinando la membresía de la comunidad
1 > membership(kc)
2 Mr Hi Actor 2 Actor 3 Actor 4 Actor 5 Actor 6
3 2 2 2 2 3 3
4 Actor 7 Actor 8 Actor 9 Actor 10 Actor 11 Actor 12
5 3 2 1 1 3 2
6 Actor 13 Actor 14 Actor 15 Actor 16 Actor 17 Actor 18
7 2 2 1 1 3 2
8 Actor 19 Actor 20 Actor 21 Actor 22 Actor 23 Actor 24
9 1 2 1 2 1 1
10 Actor 25 Actor 26 Actor 27 Actor 28 Actor 29 Actor 30
11 1 1 1 1 1 1
12 Actor 31 Actor 32 Actor 33 John A
13 1 1 1 1
La representación visual obtenida al trazar la red es
1 > plot(kc, karate)
Figura 4.2.5
La jerarquía resultante normalmente se representa en forma de un árbol, llamado dendrograma (organiza los datos en subcategorías que se van dividiendo en otros hasta llegar al nivel de detalle deseado asemejándose a las ramas de un árbol que se van dividiendo en otras sucesivamente). Este tipo de representación permite apreciar claramente las relaciones de agrupación entre los datos e incluso entre grupos de ellos, aunque no las relaciones de similitud o cercanía entre categorías. Observando las sucesivas subdivisiones podemos hacernos una idea sobre los criterios de agrupación de los mismos, la distancia entre los datos según las relaciones establecidas, etc. Como podemos ver a continuación:
1 > install.packages("ape")
2 > library(ape)
3 > dendPlot(kc, mode="phylo")
Figura 4.2.6
4.4.2 Particionamiento espectral
Un enfoque popular de ese particionamiento está basado en el análisis de le llamado laplaciano
de un grafo. El grafo laplaciano de un grafo $G$ , con matriz de adyacencia $A$ , es una matriz $L =D - A$ , donde $D = diag [( d_v )]$ es una matriz diagonal con elementos $D_{vv}= d_v$ (cuenta el
número de aristas en $E$ que inciden sobre $v$)que son las entradas de la secuencia de grado de $G$ . Un resultado formal en la teoría de grafos espectrales establece que un grafo $G$ constará de $K$ componentes conectados si y solo si $\lambda_1(L)=...=\lambda_k(L)=0$ y $\lambda_{K+1}(L)>0$, donde $\lambda_1\leq...\leq\lambda_{N_v} $ son los valores propios (no necesariamente distintos) de $L$ , ordenados de
pequeño a grande. Por lo tanto, el número de componentes en un grafo está directamente
relacionado con el número de valores propios distintos de cero del grafo laplaciano.
Se puede demostrar que el valor propio más pequeño de $L$ es idénticamente igual a cero, con el
vector propio correspondiente $x_1={(1,...,1)}^T$ . Por lo tanto, por ejemplo, si sospechamos que
un grafo $G$ consta de "casi" $K = 2$ componentes y, por lo tanto, es un buen candidato para la
bisección (división de un elemento en dos partes iguales), podríamos esperar que $\lambda_2(L)$ esté
cerca de cero. De hecho, tales expectativas son razonables, ya que el valor $\lambda_2$ está
estrechamente relacionado con una serie de medidas de conectividad y estructura del grafo. En
particular, estas relaciones indican que cuanto menor es $\lambda_2$, más fácil es que el grafo se separe
en dos subgrafos cortando un número relativamente pequeño de aristas entre los dos. Fiedler
fue el primero en asociar $\lambda_2$ con la conectividad de un grafo, sugirió dividir los vértices
separándolos según el signo de sus entradas en el vector propio correspondiente $x_2$ . El
resultado es producir dos subconjuntos de vértices (un supuesto corte).
$S=\lbrace v \in V : x_2(v) \geq 0 \rbrace$ y $\lbrace \overline{S} = v \in V : x_2(v) < 0\rbrace$
Por lo tanto, el vector $x_2$ a menudo se denomina vector de Fiedler, y el valor propio
correspondiente $\lambda_2$, valor de Fiedler. Ilustramos el uso en el grafo del club de karate
nuevamente. Es sencillo realizar el análisis-propio necesario.
1 > k.lap <- graph.laplacian(karate)
2 > eig.anal <- eigen(k.lap)
Trazamos los valores propios del grafo laplaciano.
1 > plot(eig.anal$values, col="blue",
2 + ylab="Valores propios del grafo laplaciano")
Figura 4.2.7, Autovalores del grafo laplaciano L para el grafo del club de kárate.
Notamos que (a) solo hay un valor propio exactamente igual a cero (como se esperaba, ya que
esta red es conexa) y (b) el segundo valor propio más pequeño $\lambda_2$ está bastante cerca de cero.
Extrayendo el vector de Fiedler
1 > f.vec <- eig.anal$vectors[, 33]
Y graficando las entradas de ese vector frente al número de actor
1 > faction <- get.vertex.attribute(karate, "Faction")
2 > f.colors <- as.character(length(faction))
3 > f.colors[faction == 1] <- "red"
4 > f.colors[faction == 2] <- "cyan"
5 > plot(f.vec, pch=16, xlab="Número de Actor",
6 + ylab="Entradas del vector de Fiedler", col=f.colors)
7 > abline(0, 0, lwd=2, col="lightgray")
Figura 4.2.8
En la figura observamos el vector Fiedler y su partición correspondiente (indicada por la línea
horizontal gris). Las dos facciones del club de karate (lideradas por el instructor y el
administrador, respectivamente) están indicadas en rojo y cian.
En general, por supuesto, podemos esperar que una red se divida en
más de dos subgrafos. El método de partición espectral que se acaba de describir se puede
aplicar iterativamente, primero dividiendo un grafo en dos subgrafos, luego cada uno de esos
dos subgrafos en subgrafos adicionales, y así sucesivamente. Idealmente, sin embargo, es
deseable que tales iteraciones estén destinadas a optimizar alguna función objetivo común.
4.4.3 Validación del particionamiento de grafos
Al igual que en el problema general de la agrupación de datos, la cuestión de la validación es
importante para la partición de grafos, pero a menudo no es trivial.
Por ejemplo, las proteínas que se encuentran agrupadas en un grafo de proteínas entre las acciones a menudo participan en procesos biológicos similares; de manera similar, los actores agrupados en una red social pueden compartir ciertos intereses. La partición de grafos puede verse como una herramienta para descubrir dichos subconjuntos en la ausencia de conocimiento de estas características. Cuando tengamos conocimiento de alguna noción definida externamente de pertenencia a una clase, puede ser interesante comparar y contrastar las asignaciones resultantes con las que se derivan de la partición de grafos.
4.5 Assortividad y mezcla
El enlace selectivo entre vértices, según una determinada característica (s), se denomina mezcla
selectiva en la literatura de las redes sociales. Medidas que cuantifican la mezcla selectiva en una red
dada se ha denominado assortatividad de coeficientes , y son esencialmente variaciones del concepto
de coeficientes de correlación (medida de dependencia lineal entre dos variables aleatorias
cuantitativas).
El coeficiente de assortividad en esta configuración se define como:
$$r_a=\frac{\sum_i f_{ij}-\sum_i f_{i+} f_{i+1}}{1- \sum_i f_{i+} f_{i+1}}$$
donde $f_{ij}$ es la fracción de aristas en $G$ que unen un vértice en la i-ésima categoría con un vértice en la
j-ésima categoría, $f_{i+}$ y $f_{i+1}$ denotan la i-ésima suma marginal de filas y columnas,
respectivamente, de la matriz resultante $f$. El valor $r_a$ se encuentra entre -1 y 1. Es igual a cero cuando
la mezcla en el grafo no es diferente de la obtenida a través de una asignación aleatoria de aristas que
conserva la distribución de grados marginales (distribución de probabilidad de un subconjunto de
variables aleatorias de un conjunto de variables aleatorias). Del mismo modo, es igual a uno cuando
hay una mezcla perfecta (es decir, cuando las aristas solo conectan vértices de la misma categoría). Sin
embargo, en el caso de que la mezcla sea perfectamente desasortativa (describe un grafo en el que
los vértices de grado bajo son más propensos a conectarse con vértices de grado alto.) en el sentido
de que cada arista del grafo conecta vértices de dos categorías diferentes, el coeficiente en $r_a$ no
necesariamente toma el valor -1.
Considerando nuevamente la red de interacciones proteína-proteína en la levadura. El hecho de que se
sepa que la unión física de proteínas es directamente relevante para las clases funcionales sugiere que
con frecuencia habrá una fuerte mezcla selectiva en redes de interacción proteína-proteína con
respectivas a estas clases como atributos. Por ejemplo, para la clase "P", que representa proteínas que
se sabe que desempeñan un papel en la síntesis de proteínas, vemos un coeficiente de assortividad de
casi 0,5.
1 > assortativity.nominal(yeast, (V(yeast)$Class=="P")+1,
2 + directed=FALSE)
3 [1] 0.4965229
Cuando la característica del vértice de interés es continua, en lugar de discreta, denote por $(x_e, y_e)$ los
valores de esa característica para los vértices unidos por una arista $e \in E$. Entonces, un candidato natural
para cuantificar la assortatividad en esta característica es el coeficiente de correlación de Pearson de
los pares $(x_e, y_e)$ ,
$$r = \frac{\sum_{x,y} xy (f_{xy} - f_{x+} f_{+y})}{\sigma_x \sigma_y}.$$
Aquí la suma es sobre todos los pares únicos observados $(x, y)$, con $f_{xy}$, $f_{x+}$ y $f_{+y}$ definidos en
analogía con el caso categórico, $\sigma_x$ y $\sigma_y$ son las desviaciones estándar correspondientes a la
distribución de frecuencias {$f_{x+}$} y {$f_{+y}$}, respectivamente. Un uso común del coeficiente de
assortividad $r$ es resumir la correlación grado-grado de vértices adyacentes, al estudiar la
estructura de la red. Para la red de proteínas en levadura, encontramos que el grado de correlación es
positivo y relativamente grande.
1 > assortativity.degree(yeast)
2 [1] 0.4610798
Esta observación es coherente con el análisis de la Figura 4.1.6. Donde si bien existe una tendencia a
vértices de grados más altos para enlazar con vértices similares, los vértices de grado más bajo tienden
a enlazarse con vértices de grados inferiores y superiores.
Bibliografía
[1] Kolaczyk, E. D., & Csárdi, G. (2014). Statistical Analysis of Network Data with R. Boston: Springer.
[2] Bayo, M. V. Aplicación de teoría de grafos a redes con elementos autónomos. Madrid: Universidad de Alcalá-Grado en Ingeniería en Tecnologías de las Telecomunicaciones (Escuela Politécnica Superior).
[3] M. E. J. Newman, S. Forrest, and J. Balthrop, Phys. Rev. E 66, 035101(R) (2002)
[4] Berzal, F. (s.f.). Clustering jerárquico. Granada:
DECSAI-Universidad de Granada.
Comentarios
Publicar un comentario