Capítulo 5 - Modelos matemáticos para grafos

el

Modelos matemáticos para grafos

(Extraído de: "Statistical Analysis of Network Data with R")

1. Introducción

Se realizará un cambio de enfoque en la construcción y uso de los modelos en el análisis de grafos.
Primero se empieza definiendo que un modelo de grafos se refiere a una colección de posibles grafos
$$\left\{ \mathbb{P_{\theta}\left( \mathrm{G} \right), \mathrm{G}}\in \mathscr{G}: \theta \in \Theta \right\}$$
Donde $\mathrm{G}$ es la colección de posibles grafos
$\mathbb{P_{\theta}}$ es la probabilidad en $\mathrm{G}$ 
y $\theta$ es el conjunto de valores posibles de $\Theta$

Estos modelos se utilizan en una variedad de propósitos. Como en el estudio de los mecanismos propuestos para generar características, propiedades observadas en las redes del mundo real o la evaluación de algunos factores predictivos de relaciones.

Se plantearan modelos desde distintas perspectivas que sirven para el análisis de datos de los grafos. 
  • Perspectiva matemática: Es de naturaleza mas simple y mas modificable para el análisis matemático, pero no presta atención a las técnicas estadísticas formales de ajuste y evaluación de modelos.
  • Perspectiva estadística: Esta diseñada para ajustarse a los datos, pero el análisis matemático puede ser complicado.

2. Modelos de grafos aleatorios clásicos

Un modelo de grafo aleatorio se refiere a un conjunto $\mathrm{G}$ y una probabilidad uniforme $\mathrm{P\left( \cdot  \right)}$ sobre $\mathrm{G}$ . Estos modelos son lo que mas se han desarrollado matemáticamente. 
En los artículos desarrollados por Erdös-Rényi, se planeta que la teoría clásica de los modelos de grafos aleatorios clásicos, se basan en un modelo simple en el que esta presente igual probabilidad en todos los grafos de un orden y tamaño determinado.

Su modelo especifica una coleccion de $\mathscr{G_\mathrm{N_v,N_e}}$ de todos los grafos $\mathrm{G=(V,E)}$ con $\mathrm{\left| V \right|=N_{v}}$  y $\mathrm{\left| E \right|=N_{e}}$ y la probabilidad asignada $\mathbb{P}\left(\mathrm{G}\right)=\binom{N}{N_e}^{-1}$ para cada $\mathrm{G\in \mathscr{G_\mathrm{N_v, Ne}}}$ donde $\mathrm{N=}\binom{N_v}{2}$ es el numero total de pares de vértices distintos.
Este modelo realiza la conexión de los $\mathrm{N}$ nodos con una probabilidad $\mathrm{p}$, creando un grafo con aproximadamente $\mathrm{pN\left( N-1 \right)/2}$ aristas distribuidas aleatoriamente.

Gilbert plantea una variante del del modelo, se presenta una colección $\mathrm{GN_v,p}$ que consta de todos los grafos $\mathrm{G}$ de orden $\mathrm{N_v}$ que se pueden obtener  asignando una arista independientemente de cada par de vértices distintos con probabilidad $\mathrm{p\in \left( 0,1 \right)}$. Este modelo propone el uso de dos probabilidades $\mathrm{PN}$ y $\mathrm{RN}$ para modelar el comportamiento de la red. $\mathrm{PN}$ es la probabilidad global y $\mathrm{RN}$ es la probabilidad de los enlaces existentes a partir de la construcción de un grafo aleatorio. Para calcular $\mathrm{PN}$ y $\mathrm{RN}$ se usan las siguentes ecuaciones: $\mathrm{P_N\sim 1-Nq^{N-1}}$ y $\mathrm{R_N\sim 1-2q^{N-1}}$ donde $\mathrm{N}$ es el número de nodos de la red y $\mathrm{q}$ es el grado de nodos. A este modelo se lo conoce como el modelo de Bernoulli de grafos aleatorios.

En igraph existe la función erdos.renyi.game que se puede utilizar para simular gráficos aleatorios de cualquier tipo. La figura a continuación muestra la realización de un grafo aleatorio clásico basado en la elección de $\mathrm{N_v=100}$ vértices y una probabilidad de $\mathrm{p=0.02}$ de una arista entre cualquier par de vértices. Se lo represento usando un diseño circular, y se puede ver que las aristas parecen estar dispersas entre pares de vértices de una manera bastante uniforme, como se esperaba.

  1. library(sand)
  2. set.seed(42)
  3. g.er <- erdos.renyi.game(100, 0.02)
  4. plot(g.er, layout=layout.circle, vertex.label=NA)

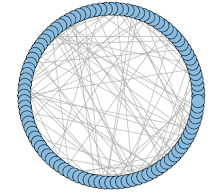Grafo aleatorio simulado de acuerdo al modelo ER

Estos grafos aleatorios no necesitan estar conectados, pero presentan una componente gigante, que contiene 71 de los 100 vértices. todos los demás componentes contienen entre uno y cuatro vértices solamente. 
  1.  table(sapply(decompose.graph(g.er), vcount))
  2.   1    2    3    4    71
  3.   15   2    2    1     1
Por lo general, un gráfico aleatorio clásico $\mathrm{G}$ tendrá una componente gigante con una alta probabilidad si $p=c/N_V$ para algún $c>1$. Bajo la parametrización para p, $c>0$, la distribución de grados estará aproximada a la distribución de Poisson, con media $c$, para $N_v$ grandes.  Esto es algo fácil de ver a un nivel intuitivo, ya que el grado de cualquier vértice dado se distribuye como una variable binomial aleatoria, con parámetros $N_v -1$ y $p$ . Sin embargo la prueba formal de este resultado no es trivial. En el libro de Bollobás se puede encontrar una referencia estándar para este y otros resultados similares.  En el grafo simulado, el grado medio esta bastante cerca del valor esperado de $(100 - 1) * 0.02 = 1.98$
  1. mean(degree(g.er))
  2. [1] 1.9
Ademas de que, el ejemplo, presenta una distribución de grados homogénea. 

Distribución de grados de ejemplo anterior

Otras propiedades de los grafos aleatorios clásicos indican que hay relativamente pocos vértices en las rutas mas cortas entre pares de vértices.
  1. average.path.length(g.er) 
  2. [1] 5.276511 
  3. diameter(g.er) 
  4. [1] 14
y cuan bajo es el agrupamiento o clustering.
  1. transitivity(g.er) 
  2. [1] 0.01639344

3. Modelos de grafos aleatorio generalizados

El modelo ER se puede generalizar de una manera directa. La receta básica es:
  1. Definir una colección de grafos $\mathscr{G}$ que consiste en todos los grafos de un $N_v$ de orden fijo que poseen una o unas características determinadas.
  2. Asignar la misma probabilidad a cada uno de los grafos $\mathrm{G\in \mathscr{G}}$. 
La característica más comúnmente elegida es la de una secuencia de grados. a diferencia del modelo ER. Existe una función en igraph llamada degree.sequence.game que se puede utilizar para muestrear de manera uniforme grafos aleatorios con una secuencia de grados fija. Por ejemplo, si se esta interesado  en los grafos de los vértices de $N_v=8$, la mitad de los cuales tienen el grado $d=2$, y la otra mitad, grado $d=3$. Dos ejemplos de tales grafos, dibujados uniformemente a partir de colección de todos estos grafos, se muestran a continuación:
  1. degs <- c(2,2,2,2,3,3,3,3)
  2. g1 <- degree.sequence.game(degs, method="vl")
  3. g2 <- degree.sequence.game(degs, method="vl")
  4. plot(g1, vertex.label=NA)
  5. plot(g2, vertex.label=NA) 

Grafos $g1$ y $g2$ dibujados uniformemente de la colección de todos los grafos $G$ con $N_v=8$ vértices y secuencia de grados (2,2,2,2,3,3,3,3).
Estos grafos no son isomorfos, es decir que no son grafos matemáticamente iguales, no se mantienen las adyacencias, estructura, caminos ni ciclos. Para un número fijo de vértices $N_v$, la colección de grafos aleatorios con todas las secuencias de grados tiene el mismo número de aristas $N_e$, debido a la relación $d = 2N_e / N_v$, donde $d$ es el grado medio de la secuencia $(d (1), ..., d (N_v))$.
  1. graph.isomorphic(g1, g2) 
  2. [1] FALSE
  3. c(ecount(g1), ecount(g2)) 
  4. [1] 10 10
Por lo tanto, esta colección está estrictamente contenida dentro de la colección de gráficos aleatorios $\mathscr{G_\mathrm{N_v,N_e}}$, con el número correspondiente $N_v, N_e$ de vértices y aristas.
Por otro lado, es importante tener en cuenta que todas las demás características son libres de variar en la medida permitida por la secuencia de grados elegida.

En principio, es fácil restringir aún más la definición de la clase $\mathscr{G}$, de modo que se fijen características adicionales más allá de la secuencia de grados. Los métodos de la cadena de Markov Monte Carlo (MCMC) son populares para generar grafos aleatorios generalizados $G$ a partir de tales colecciones, donde los estados visitados por la cadena de Markov son los propios grafos $G$ distintos. McDonald, Smith y Forster, ofrecen algoritmos MCMC para varios casos diferentes, como cuando los grafos $G$ están dirigidos y restringidos para tener un par fijo de entradas y salidas, secuencias de grados y un número fijo de aristas mutuos. Sin embargo, el diseño de tales algoritmos en general no es trivial.

Los métodos de la cadena Markov Monte Carlo (MCMC) comprenden una clase de algoritmos para el muestreo a partir de una distribución de probabilidad mediante la construcción de una cadena Markov.

4. Modelos de grafos basados en mecanismos

Los modelos de grafos basados en mecanismos fueron una de la innovaciones mas grandes en el modelado moderno de redes. Estos modelos están diseñados explícitamente para imitar ciertas propiedades observadas del mundo real, a menudo mediante la incorporación de mecanismos simples.

4.1. Modelos de mundo pequeño

En muchas redes del mundo real se muestran altos niveles de agrupación, pero pequeñas distancias entre la mayoría de los nodos. Tal comportamiento no puede ser reproducido por gráficas aleatorias clásicas,  puesto que el diámetro escala logarítmicamente indicando distancias pequeñas entre nodos y el coeficiente de agrupamiento sugiere muy poco agrupamiento.

Watts y Strogatz plantearon la idea de un grafo con estructura de rejilla o malla que básicamente es una estructura en red de barras rectas interconectadas en nudos formando triángulos planos y luego recablear aleatoriamente un pequeño porcentaje de los bordes para representar las redes del mundo real. 

Este modelo parte de un conjunto de $N_v$ vértices, dispuestos de forma periódica, y se une cada vértice $r$ a sus vecinos a cada lado. Luego, para cada arista, independientemente y con probabilidad $p$, un extremo de esa arista se moverá para incidir en otro vértice, donde ese nuevo vértice se elige de manera uniforme, pero con atención para evitar la construcción de bucles y multi-aristas.

Recableado de una malla regular hasta llegar al modelo de Watts y Strogatz

Un ejemplo de un grafo de mundo pequeño de este tipo se puede generar en igraph usando la función watts.strogatz.game.
  1. g.ws <- watts.strogatz.game(1, 25, 5, 0.05) 
  2. plot(g.ws, layout=layout.circle, vertex.label=NA)
  3. transitivity(g.ws)
  4. [1] 0.5122592
Esta imagen es el modelo WS planteado anteriomente con $N_e=25$ vértices, vecindarios de tamaño $r = 5$ y probabilidad de recableado $p = 0.05$ . Además se observa un agrupamiento alto.

Si se crea un grafo con la probabildad de recableado de $p=0$, el coeficiente de agrupamiento seria de $0.6666667$ pero la distancia entre vertices no es trivial $5.454545$

  1. g.lat100 <- watts.strogatz.game(1, 100, 5, 0) 
  2. transitivity(g.lat100) 
  3. [1] 0.6666667
  4. diameter(g.lat100) 
  5. [1] 10 3
  6. average.path.length(g.lat100) 
  7. [1] 5.454545
El efecto de recablear un número relativamente pequeño de bordes de forma aleatoria es reducir notablemente la distancia entre los vértices, mientras se mantiene un nivel de agrupamiento igualmente alto.

4.2. Modelos de fijación preferencial

Las redes del mundo real evolucionan con el tiempo, y así se pueden configurar los grafos para imitar este comportamiento de crecimiento de red. Por lo general,  se especifica un mecanismo o mecanismos simples sobre cómo cambia la red en un momento dado, según conceptos como preferencia de vértice, aptitud, copia, edad y similares. Un ejemplo de un mecanismo es el del apego preferencial, diseñado para incorporar el principio de que "los ricos se hacen más ricos". El trabajo de Barabasi y Albert presenta una fascinación por la introducción de mecanismos para reproducir los tipos de distribuciones de grado amplio.

El modelo de Barabasi-Albert (BA) para gráficos no dirigidos se formula de la siguiente forma: 
  • Comienza con un grafo inicial $G^{(0)}$ de $N_v^{(0)}$ vértices y $N_e^{(0)}$ aristas.
  • Luego, en la etapa $t=1,2,3,...$ el grafo actual $G^{(t-1)}$ se modifica para crear un nuevo gráfico $G^{(t)}$ agregando un nuevo vértice de grado $m>=1$, donde las nuevas aristas están unidas a $m$ vértices diferentes en $G^{(t-1)}$. La probabilidad de que el nuevo vértice se conecte a un vértice $v$ dado, esta dada por $\frac{{d_{v}}}{\sum_{{v}'\in V}^{}d_{v'}}$
  • Es decir que, en cada etapa, $m$ vértices existentes se conectan a cada nuevo vértice de manera preferencial a aquellos que tienen grados mas altos. 
  • Después de $t$ iteraciones, el grafo resultante $G^{(t)}$ tendrá $N_v^{(t)}=N_v^{(0)}+t$ vértices y $N_e^{(0)}=N_e^{(0)}+tm$ aristas. 
Debido a la tendencia hacia el apego preferencial, se esperaría que una serie de vértices de grado comparativamente alto emergieran gradualmente a medida que $t$ aumenta. 

En igraph, usando la función barabasi.game, se puede simular un grafo aleatorio BA. Por ejemplo, $N_v = 100$ vértices, con $m = 1$ nuevas aristas agregadas para cada nuevo vértice.
  1. set.seed(42)
  2. g.ba <- barabasi.game(100, directed=FALSE)
  3. plot(g.ba, layout=layout.circle, vertex.label=NA)
Grafo aleatorio con el modelo BA descrito anteriormente.
Se debe tener en cuenta que las aristas se distribuyen entre pares de vértices de una manera decididamente menos uniforme que en el gráfico aleatorio clásico (Grafo aleatorio de Erdös-Rényi). Y, de hecho, parece haber vértices de un grado especialmente alto, los denominados vértices concentradores. 
  1. hist(degree(g.ba), col="lightblue", xlab="Grado", ylab="Frequencia", main="")
Gráfico de distribución del grafo del ejemplo anterior
Se observa que la distribución global es heterogénea. La mayoría de los vértices no tienen un grado superior a 2 y por otro lado solo un vértice tiene un grado 9.
  1. summary(degree(g.ba))
  2. Min.  1st Qu.  Median   Mean   3rd Qu.   Max. 
  3. 1.00   1.00      1.00        1.98      2.00       11.00
Los grafos generados según el modelo BA comparten la tendencia hacia poseer relativamente pocos vértices en las rutas más cortas entre pares de vértices y bajo agrupamiento
  1. average.path.length(g.ba)
  2. [1] 4.923434 
  3. diameter(g.ba) 
  4. [1] 9 
  5. transitivity(g.ba) 
  6. [1] 0

5. Evaluación de la importancia de las características de los grafos

Los modelos anteriores son demasiado simples para un modelo estadístico serio con redes observadas, pero desde una perspectiva de prueba de hipótesis estadística presentan un papel útil en el análisis de redes. Específicamente, los modelos de grafos presentados en el presente capitulo se utilizan con frecuencia en la evaluación de la importancia de las características de los grafos.

5.1. Evaluación del número de comunidades en una red

Los métodos de Monte Carlo, que utilizan algunas de las mismas funciones R encontradas anteriormente, nos permiten generar rápidamente aproximaciones a las distribuciones de referencia correspondientes. Para hacerlo, necesitamos el orden, el tamaño y la secuencia de grados de la red.

Se generan aproximaciones a las distribuciones de referencia y luego procede a generar grafos aleatorios clásicos de este mismo orden y tamaño para cada uno, Se usa el mismo algoritmo de detección de comunidades para determinar el número de comunidades. 

  • Al definir nuestro marco de referencia usaremos dos opciones de G:
  • Grafos del mismo orden 
  • Grafos que obedecen a la restricción adicional de que tienen la misma distribución de grados como el original. 
Para ejemplificar, se necesita el orden, el tamaño y la secuencia de grados de la red de karate original. Y luego se procede a generar grafos aleatorios clásicos de este mismo orden y tamaño, se hace lo mismo usando grafos aleatorios generalizados restringidos para tener la secuencia de grados requerida. Los resultados se pueden resumir y comparar utilizando gráficos de barras lado a lado


Distribución del número de comunidades detectadas para grafos aleatorios del mismo tamaño (azul) y secuencia de grados (rojo) que la red de karate.

Se concluye que es probable que exista un mecanismo adicional en funcionamiento en el grafo real, uno que va más allá de la simple densidad y distribución de las interacciones sociales en esta red.

5.2. Evaluación de las propiedades de mundo pequeño

La noción de redes de mundo pequeño ha sido particularmente popular en el campo de la neurociencia, donde numerosos autores han presentado evidencia para argumentar que el comportamiento de mundo pequeño se puede encontrar en varias representaciones del cerebro basadas en redes.

Para poder evaluar el comportamiento de un mundo pequeño se compara el coeficiente de agrupamiento observado y la longitud del camino promedio en una red observada  con lo que podría observarse en un grafo aleatorio clásico calibrado adecuadamente. 

Si la red que se esta observando exhibe un comportamiento en que el coeficiente de agrupamiento 
observado exceda el de un grafo aleatorio, mientras que la longitud de la ruta promedio permanece aproximadamente igual.

Para evaluar el agrupamiento en esta red, se usa una extensión a los grafos dirigidos del coeficiente de agrupamiento, y esta cantidad se define como el promedio sobre todos los vértices v de los coeficientes de agrupamiento específicos del vértice.
$$cl(v)=\frac{(A+A^{t})^{3}_{vv}}{2[d_{v}^{tot}(d_{v}^{tot}-1)-2(A^{2})_{vv}]}$$
Donde $A$ es a matriz de adyacencia y $d_v^{tot}$ es el grado total, es decir, el grado de entrada mas el grado de salida del vertice $v$.

Las longitudes de las rutas se definen en esta red solo para rutas dirigidas. Los pasos necesarios para simular los dibujos de grafos aleatorios clásicos (dirigidos) y para evaluar el agrupamiento y la longitud del camino promedio para cada uno son análogos.
    • Por un lado, hay sustancialmente más agrupaciones en la red de lo que se esperaba de una red aleatoria.
    • Por otro lado, los caminos más cortos entre pares de vértices son notablemente más largos.
    • Por lo tanto, la evidencia del comportamiento del mundo pequeño en esta red no es clara, con los resultados ya que se comporta como un grafo aleatorio clásico.
Bibliografía

[1] Kolaczyk, E. D., & Csárdi, G. (2014). Statistical Analysis of Network Data with R. Boston: Springer.




Comentarios

Publicar un comentario